Computing the convection coefficient of a brake disc

Back in college, in 2017, I was part of the Formula Student team of Politecnico di Torino. I was tasked with designing several Unsprung Mass components, including the brake discs.

The Team didn't have any data recorded from previous years about the temperatures of the brakes during a race. As you can imagine, knowing this would be a great advantage when dimensioning the brake discs.

Not having the temperature data, I estimated the temperatures using a lumped mass approach.

However, a key parameter you need for doing that is the convection coefficient.

But, how do you find it?

Let me show you how I did it, and what I learned when comparing the results with real-world data.

Many options, limited resources

To figure out the heat transfer coefficient of a brake rotor, the most realistic approach would be to perform an experimental study and obtain an empirical correlation applicable to the flow conditions in the wheels of the Formula SAE car.

This means time and instrument$ that we didn't have available at the time.

The next method would be to set up a Computational Fluid Dynamics (CFD) study to analyze the heat transfer between the disc brakes and the environment.

However, setting up a reliable CFD study is time-consuming, and would require additional time to learn how to properly utilize the computational tools. The guys working on aero design were already quite busy figuring out the new car, so it was not feasible to ask them for a detailed study of the previous car, just to find the convection of the brake discs.

So there is the third option: analytical determination. Heat transfer is full of empirical correlations. E.g. "formulas" that work, just because they do. They were found experimentally in some controlled environment, and are applicable to describe the heat transfer in similar situations.

So this is the approach I followed - I needed to start somewhere, right?

Decomposing the problem

To use the empirical correlations available in the literature, I "split" the problem into the following basic cases for heat convection:

Cylindrical body

I considered the outer edge of the brake discs as a cylindrical body with a length equal to the thickness of the rotor.

The air was considered as flowing around the cylindrical edge at the vehicle speed and the average Nusselt number was obtained using Hilpert's correlation for flows over cylinders[2]. It is valid for Prandtl numbers greater or equal to 0.7.

\[\overline{h_{c y l}}=\frac{C R e_D^m P_f^{1/3} k_{a i r_f}}{2 r_{d i s c}}\]

Planar body

The sides of the brake disc were considered as a planar plate with a length much greater than the rotor thickness.

The airflow at the vehicle speed is assumed to be parallel to the surface. For laminar flows, the plate is considered to be isothermal and the average heat transfer coefficient can be obtained from[1]

\[\overline{h_{\text {plate }}}=\frac{0.664 {Re_L}^{1 / 2} {Pr_f}^{1 / 3} k_{\text {airf }}}{2 r_{\text {disc }}}\]

For turbulent flows, the plate can be assumed to have a constant heat flow and the average heat transfer coefficient is given by

\[\overline{h_{\text {plate }}}=\frac{0.680 {Re_L}^{1 / 2} {Pr_f}^{1 / 3} k_{\text {airf }}}{2 r_{\text {disc }}}\]

Rotating thin disc

For this case, I neglected the thickness of the brake disc. I computed the heat transfer coefficient for the friction ring using the empirical correlation proposed by Latour, Bouvier and Harmand [4]. It applies for a rotating thing disc with transverse air crossflow:

\[ \overline{h_{rot}}=\frac{\sqrt{{\lparen 0.036 {Re_{U}}^{0.8} \rparen}^2+{\lparen 0.556 {Re_{\omega}}^{0.5} \rparen}^2} k_{air_{f}}}{2 r_{disc}} \]

Only valid when

\[\frac{Re_\omega}{Re_L} > 0.18\]

The subscript f in these expressions means that the air properties and the flow conditions are evaluated at the so-called film temperature.

Combining the contributions from different shapes

I evaluated the correlations above for a range of vehicle speeds.

Then, I combined them to obtain an "equivalent" heat transfer coefficient considering the relative surfaces applicable for each one of them. It's like a weighted sum:

· The cylindrical body simplification was only associated with the small area around the edge of the rotor,

\[A_{edge} = 2 \pi r_{outer} t_{disc}\]

being t_disc the thickness of the disc, and r_outer its outer radius.

· The coefficients obtained from the flat plate and the rotating thin disc assumptions were related to the side area of the discs, A_side, including the surface area of the attachments between the rotor and the disc carrier.

Finally, I defined the equivalent heat transfer coefficient as

\[\overline{h_{\text {equiv }}}=\left(\overline{h_{\text {rot }}}+2 \overline{h_{\text {plate }}}\right) R_{\text {side }}+\overline{h_{c y l}} R_{\text {edge }}\]

where

\[R_{\text {side }}=\frac{A_{\text {side }}}{2 A_{\text {side }}+A_{\text {holes }}+A_{\text {edge }}}\]

and

\[R_{\text {edge }}=\frac{A_{\text {edge }}}{2 A_{\text {side }}+A_{\text {holes }}+A_{\text {edge }}}\]

Additionally, I evaluated another experimental correlation for approximating the heat transfer coefficient of non-ventilated disc brakes mentioned in Brakes Design and Safety by Rudolf Limpert [1].

\[h=0\ldotp 04\left(\frac{k_{\mathrm{air}} }{D}\right){\mathrm{Re}}^{0\ldotp 8}\]

It was obtained from experiments performed on a light truck.

Convection at different speeds

I plotted the results obtained when evaluating these correlations for different vehicle speeds, for a constant disc temperature of 150°C.

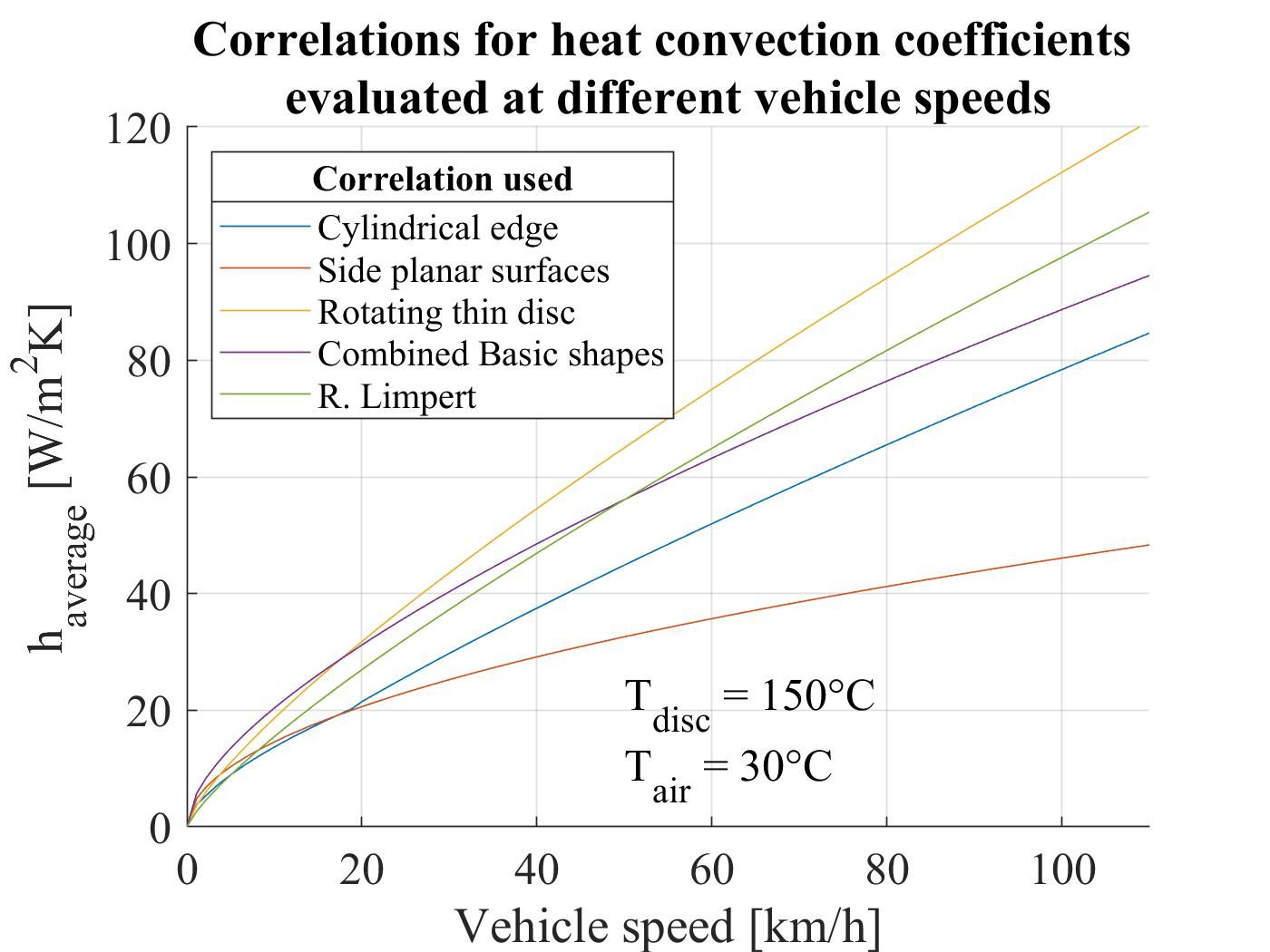
I considered the magnitude of the air velocity around the brake disc as equal to that of the vehicle speed, which was increased linearly from 0 to 110 km/h. This is an oversimplification, of course, but remember, I had no reference data when starting out.

To do this, I calculated the Reynolds number Re_L=Re_U=Re_D at each speed value. I also computed the rotational Reynolds number Re_ω at the angular speed of the rotor corresponding to each vehicle speed.

At 60 km/h, the combined effect of the different correlations for basic shapes provided a value of 58 W/m2K. Later on, CFD analyses showed similar values at the same speed.

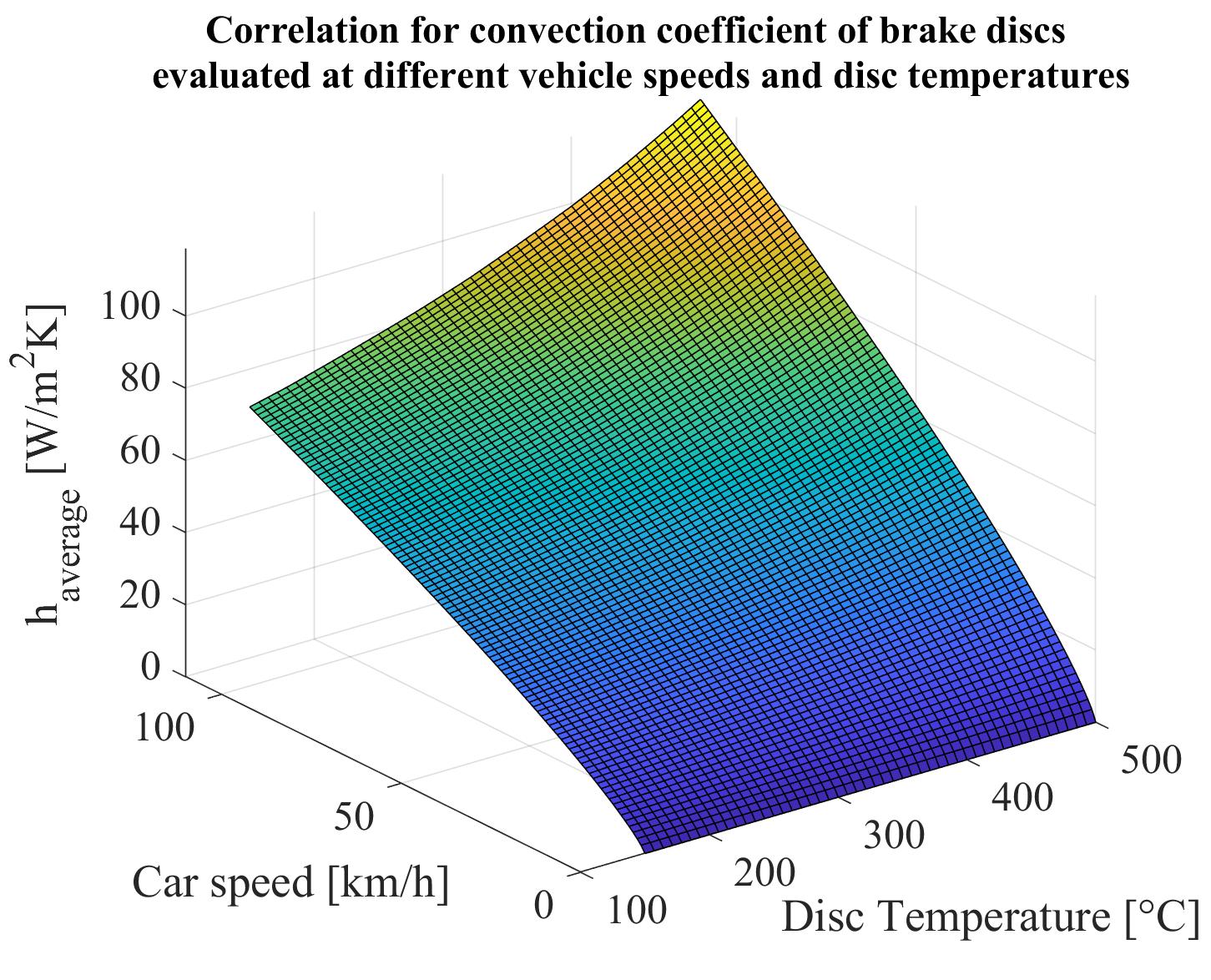
How accurate is this?

Well, that's the hard question, of course.

After the initial estimates, some of the guys from the Aerodynamics division of Squadra Corse Polito 2017 ran a CFD study to evaluate the convection coefficient of the brakes.

The analysis was set considering the flow field around the rotating wheels obtained from a previous full-vehicle simulation with an air speed of 60 km/h.

A constant surface temperature of 300°C was assigned to the brake disc and the caliper was assumed to be an adiabatic body.

You can see the results below. It shows the heat flux contour plots on the side of the disc facing toward the vehicle center.

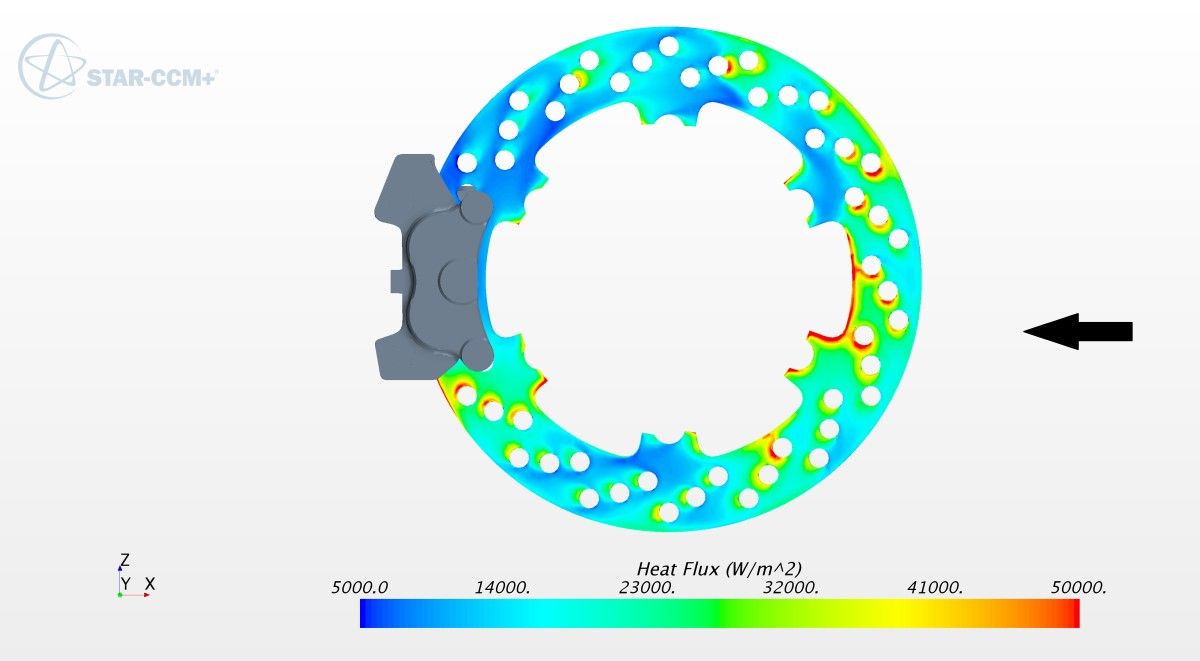
Considering that the total surface area of the brake disc was 0.0437 m² and the total power exchange with the fluid was approximately 678 W, the average heat transfer coefficient was around 60 W/m²K.

This was close to the analytical results! as you can see in the figures of the previous section.

Can I use this to estimate brake disc temperature?

There is no simple answer. In short, yes, but there are some really important caveats.

When I obtained these results I was on one side happy because they matched the results from a CFD study, even though I simply combined a bunch of empirical correlations from the literature.

On the other side, I was worried, because using them to estimate the temperatures of the discs during a race using real data yielded high temperatures.

I used some CAN data from the previous car to estimate the temperatures of the brake discs, using a similar approach to the one I described here, but this time I was using real wheel speeds recorded for an actual race.

You can see the results for an Endurance race below.

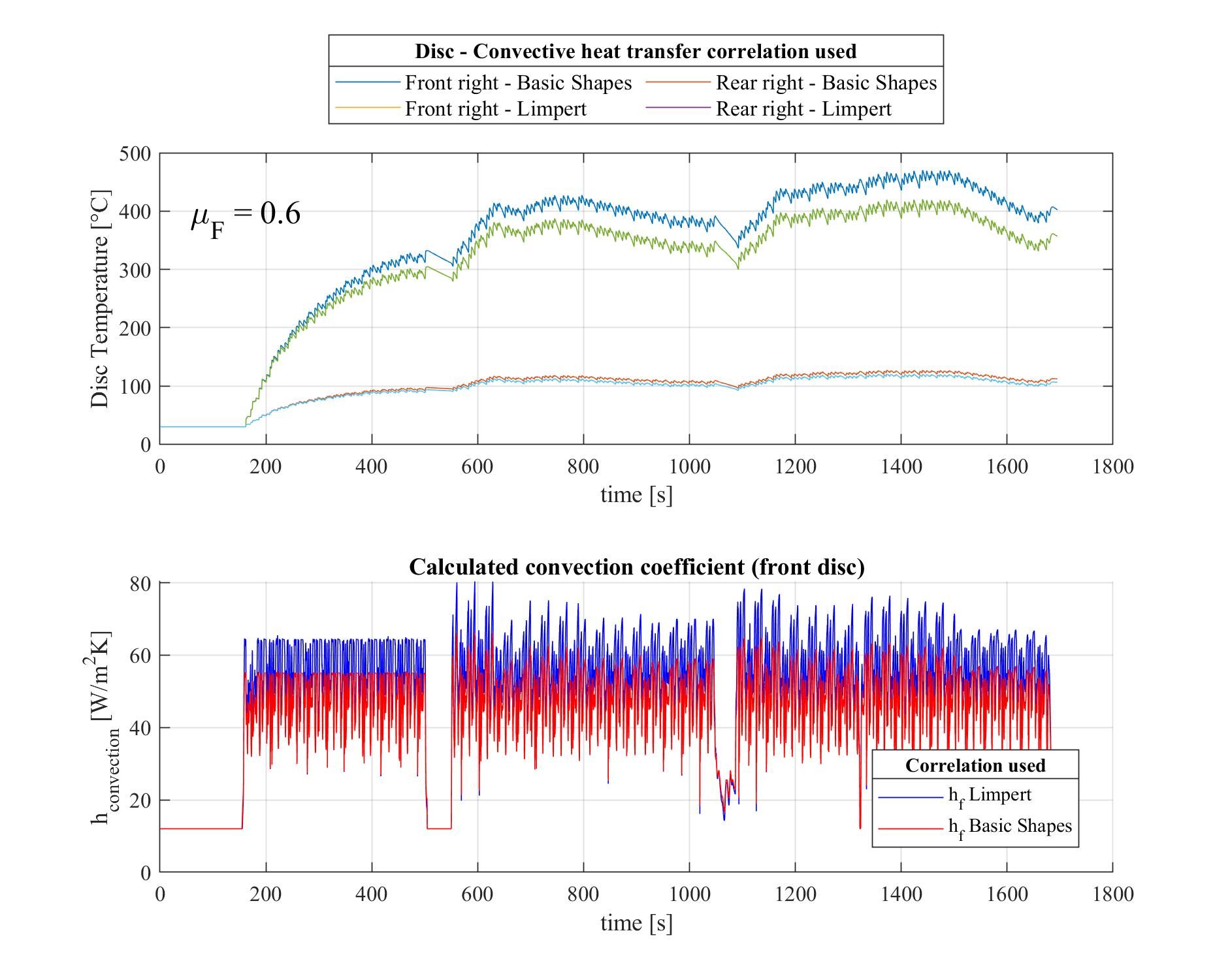
I was doubtful, and other guys within the Team were also very hesitant to trust the results.

It can't be. The brakes would've faded.

We resorted to the literature to find other reference values. At the time, there were papers online (like this one and this one) showing convection coefficients for formula SAE cars in the order of 200 W/m2K, so we decided to use higher values for our simulations, since "the results made more sense".

Unfortunately, this was just silly cherry-picking, and attempting against all good engineering practices

Later on, we found that the discs did reach the high-temperature values.

We still couldn't measure the temperatures while running, but we used thermal paints to see whether the peak values reached different thresholds.

The change in color from green to white indicates that the maximum temperature that the discs surpassed 430°C during the Endurance event.

Are the estimated temperatures accurate?

No way to tell from these results. We just got an indication of the peak temperatures, but have no idea about the actual trend.

The problem with estimating the disc temperature using CAN data (with no actual temperature measurements to use as reference) is that there is too much uncertainty around key parameters for the calculation of the disc temperature, besides the heat convection coefficient.

For example:

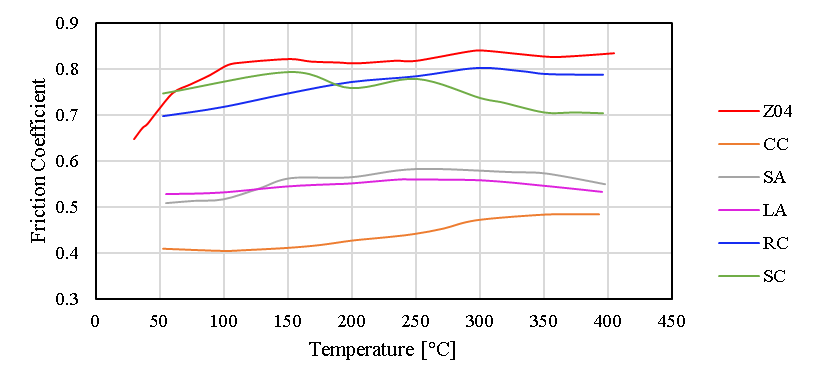
1. The friction coefficient between the discs and brake pads

The data from the manufacturer indicated a value of 0.8 at 400 °C. However, it seemed too high.

If it was that high, then the car would've been able to brake at a much higher rate.

If I computed the temperatures of the discs using this coefficient, the results would've been simply not plausible for a Formula Student car.pad

The results shared by brake pad manufacturers are only useful for a comparative evaluation of brake pads tested under similar laboratory conditions.

Those conditions are unlikely to be present during a real race, so the actual coefficients you'd see in real life are much lower.

2. Heat partition coefficient during braking

As I've mentioned before, this heat partition coefficient determines the proportion of the total heat that is transferred to the rotor while braking.

It is not easy to estimate it. Assume a value too high, and the estimated temperature of the discs will be higher than the real ones.

3. Rolling resistance

When calculating the temperature of a brake disc, you essentially perform an energy balance. If you neglect some effects from it, you obviously get altered results.

This is the case with the rolling resistance of the tires, which I did not include when making the simulations for estimating the average disc temperature with a lumped mass approach.

Similar to the aerodynamic energy (drag times distance), the rolling resistance "favors" the deceleration of the car. Not including it is like artificially increasing the amount of heat that is dissipated by the brakes when braking. This results in higher temperatures, of course.

Conclusion

Estimating the convection heat transfer coefficient for a brake disc is possible. If we don't have actual temperature data, we can use empirical correlations or CFD studies to get some results.

However, we have to be careful about what assumptions we are making when doing so. What are we going to use the results for?

Nothing beats experimental validation, especially for heat transfer problems like this.

I just hope you found something interesting when reading this, and maybe use some of this for your own projects - bearing in mind all the caveats I mentioned.

References: